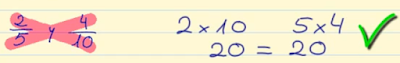viernes, 10 de mayo de 2019
sábado, 16 de marzo de 2019
miércoles, 31 de octubre de 2018
1.1. Números racionales
Número racional es todo número que puede representarse como el cociente de dos números enteros.
Representación gráfica de las fracciones cuyo divisor es 4.
- Es una fracción común con numerador y denominador distinto de cero.
- El término «racional» alude a una fracción o parte de un todo.
- El conjunto de los números racionales se denota por Q que deriva de «cociente» (Quotient ).
- Este conjunto de números incluye a los números enteros (), y es un subconjunto de los números reales ().
1.1.1. Fracciones
equivalentes
Las fracciones equivalentes son aquellas fracciones que representan la misma parte de una unidad.
Las fracciones equivalentes son aquellas fracciones que representan la misma parte de una unidad.
- Si dos fracciones son equivalentes, el producto de los extremos es igual al producto de los medios.
¿Como podemos calcular fracciones equivalentes?
- Por amplificación: Multiplicando numerador y denominador por el mismo número.
- Por simplificación: Dividiendo numerador y denominador por un divisor común entre ambos.
Por ejemplo, 12/30 podemos dividir el numerador y el denominador entre 2, ya que tanto el numerador como el denominador son pares.
El conjunto de los números racionales (Q) es el conjunto de números que se pueden escribir de la forma a/b, donde a y b son números enteros con b ≠ 0.
1.1.3. Orden en los números racionales
Orden de los Números Racionales: mayor, menor o igual
Al igual que los números enteros, los números racionales también pueden ser localizados en la recta numérica para su ordenación. Por ejemplo, en la figura 5 se muestran los números racionales y .
Se observa que el número se encuentra a la izquierda de , por lo que es menor que , es decir:
Utiliza
el siguiente recurso GeoGebra para comparar diferentes números racionales. Para
ello modifica los valores del numerador y del denominador, observa su
representación en la recta numérica y compáralos. Hazlo seleccionando:
- Números positivos
- Números negativos
- Un número positivo y otro negativo.
Observa
que su posición en la recta numérica determina la relación de orden entre los
números, tal como ya analizamos con anterioridad. Un número es menor si se
encuentra a la izquierda de un segundo número; será mayor si se encuentra a la
derecha; y ambos números serán iguales si ocupan el mismo lugar en la recta
numérica.
Referencias bibliograficas:
- https://es.wikipedia.org/wiki/Número_racional
- https://www.smartick.es/blog/matematicas/fracciones/fracciones-equivalentes/
- https://sites.google.com/site/cursomatematicasparanegocios1/sesion-9-1
- https://www.youtube.com/watch?v=hfFkEVvZmKU
- https://portalacademico.cch.unam.mx/alumno/matematicas1/unidad1/comparacionEntreCantidades/RDONumerosRacionales
- https://es.wikibooks.org/wiki/Números_y_Operaciones/Números_Racionales/Relaciones_de_equivalencia
martes, 30 de octubre de 2018
1.2. Expresiones fraccionaria y decimal de un número racional
1.2. Expresiones fraccionaria y decimal de un número racional
El porcentaje es un tipo de comparación entre dos cantidades: una indica la parte o un total y la otra corresponde al total o unidad. Entonces, todo porcentaje se puede escribir como una fracción.
1.2.1. Expresión decimal de un número racional
La expresión decimal equivale a la división del numerador entre el denominador.
Para escribir un fracción decimal en forma de número decimal, se escribe el numerador y se separan con una coma, hacia la derecha, tantas cifras decimales como ceros tenga el denominador. si es necesario se añaden ceros.
1.2.3. Fracción generatriz de un número racional
Fracción generatriz de una expresión decimal periódica mixta
Referencias bibliograficas:
Fracción generatriz de una expresión decimal exacta
La fracción generatriz de una expresión decimal exacta es aquella cuyo numerador es igual a la parte entera seguida por la parte decimal (sin la coma) y el denominador es una potencia de 10, con tantos ceros como cifras decimales tiene el número.
Fracción generatriz de una expresión decimal periódica pura
La fracción generatriz de una expresión decimal periódica pura con parte entera nula tiene por numerador el periodo y por denominador el número formado por tantos nueves como cifras tenga el periodo. Si el número tiene parte entera distinta de cero, se calcula la fracción generatriz de la parte decimal y después se le suma la parte entera.
La fracción generatriz de una expresión decimal periódica mixta con parte entera nula tiene por numerador un número formado por el anteperiodo seguido del periodo, menos el anteperiodo; tiene por denominador un número con tantos nueves como cifras tenga el periodo, seguido de tantos ceros como cifras tenga el anteperiodo. Si el número tiene parte entera distinta de cero, se calcula la fracción generatriz de la parte decimal y después se le suma la parte entera.
Referencias bibliograficas:
lunes, 29 de octubre de 2018
1.3. Números racionales en la recta numérica
1.3. Números racionales en la recta numérica
Para representar un racional en la recta numérica, se dividen las unidades en tantas partes como indica el denominador y se toman tantas como indica el numerador. Los racionales negativos toman las partes hacia el lado izquierdo del cero.
Para poder representar los números racionales en la recta numérica, se debe ubicar un punto origen, 0, y un punto para designar la unidad 1. A partir de esta unidad se construyen los números enteros, replicando esta distancia hacia la derecha para los positivos o hacia la izquierda para los negativos.
Referencias bibliográficas
domingo, 28 de octubre de 2018
1.4. Operaciones con números racionales
1.4. Operaciones con números racionales
Para resolver ciertas situaciones, es necesario aplicar operaciones entre racionales, tales como la adición, la sustracción, la división, la multiplicación y la potenciación.
Si a, b, c, d ∈ Z, con b y d ≠ 0, y m, n ∈ N, entonces las operaciones con números reales se pueden definir como se muestra a continuación.
Referencias bibliográficas
sábado, 27 de octubre de 2018
1.5. Números irracionales
1.5. Números irracionales
Los números irracionales son aquellos que no se pueden expresar como razones entre números enteros y tienen como característica que su expresión decimal es infinita no periódica. Este conjunto se representa con el símbolo I.
En el conjunto de los números irracionales encontramos todas las raíces que no son exactas. Además, entre los números irracionales encontramos números especiales como el número áureo o el número de Euler.
1.5.1. Números irracionales en la recta numérica
Referencias bibliográficas
Suscribirse a:
Entradas (Atom)